Author: Jason Marks
The URQLE Equation
The URQLE equation (Unified Quantum Relativistic Lagrangian Equation) is designed to model complex interactions in quantum systems, encompassing relativistic effects, wave-particle duality, and multi-dimensional interactions. This equation serves as a foundation for analyzing quantum states, entanglement, and multi-field dynamics in a unified framework.
The equation can be presented as follows:
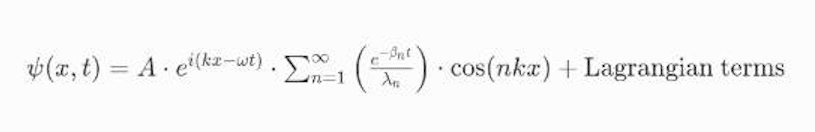
Where:
- ψ(x,t) represents the quantum state of particles in a multi-dimensional space.
- A is the amplitude, providing the initial energy configuration of the system.
- k (wave number) and w angular frequency) account for wave-like properties within the system.
- βn is a decay constant, associated with quantum state transitions over time.
- λn represents the lattice constant or a scaling factor for dimensional interactions.
The Lagrangian terms introduce relativistic and field-related components that modify particle interactions based on the external field configurations, such as gravitational fields or electromagnetic fields within the system.
Explanation and Description
The URQLE equation integrates quantum and relativistic properties, offering a unified framework to:
- Describe Quantum Wave Interactions: The wave function component captures the probabilistic nature of particles and how they oscillate and decay over time.
- Model Relativistic Effects: The Lagrangian component allows the inclusion of relativistic corrections to account for high-energy, high-velocity effects, essential for accurate modeling in cosmological and quantum field settings.
- Multi-Dimensional Interactions: With λn as a lattice constant, the URQLE equation can adapt to higher-dimensional spaces and tensor fields, making it suitable for higher-dimensional quantum field models.
- Quantum State Decay: By observing how βn affects the exponential decay term, the equation shows how quantum states evolve and decay over time, revealing the transient nature of specific configurations in high-energy systems.
- Relativistic Adjustments in High-Field Systems: The Lagrangian terms accommodate variations in field intensity, showing how particle states are altered when exposed to significant gravitational or electromagnetic fields.
- Multi-Dimensional Wave Functions: The inclusion of λn allows for flexible adaptations across dimensions, permitting the modelling of wave-particle interaction and multi-dimensional configuration.
